三角 関数 定義 厳密
Sumifs 関数 数学三角関数の 1 つ は複数の検索条件に一致するすべての引数を合計しますたとえば1 ある 1 つの郵便番号区域に所在しており2 利益が特定の金額を超える国内の販売店の数を合計するときなどにsumifs 関数を使います. 三角関数のべき乗をsin2 xなどと表すことは一般的ですが微妙です少し手間ですがsin x2と書いた方が紛らわしさはなくなりますsin x2と区別できている 三角関数の逆関数が存在することは厳密には次のようにして示せます.
三角関数y Sin8について 厳密な定義を教えてください Yahoo 知恵袋

三角関数の加法定理とその証明 おいしい数学
O9tex6k1tydsm
この関数は Barnes 以来多くの数学者が同等の定義を行うが特に新谷卓郎によるモジュラー形式との関係の研究黒川信重による Selberg ゼータ関数のガンマ関数因子に関する研究など数論への応用を経て次第に注目されるようになり現在では多重三角関数と言えば大抵この関数を指すよう.
三角 関数 定義 厳密. 指数関数 を一意的に定義するための特徴付けは同値な方法がいくつも知られている 中でも以下の冪級数. この時足し合わせるのは様々な理論上は無限の種類の周波数をもつ三角関数を足し合わせる必要があります例えば高校で出てくる3倍角の公式 cos3t dfrac14 cos3t dfrac34. こんにちはウチダです 今日は数学Ⅱで初めて登場するが詳しくは数学Ⅲで習う 漸近線 について求め方意味定義について解説していきます 主な具体例分数関数や双曲線も挙げながら詳しく見ていきましょう 漸近線とは まずは聞き慣.
1 複素数と指数関数 本章のあらまし まず高校で学んだ複素数と複素数平面に対して厳密 な定義を与えその存在を確認しようまた基本的な計 算規則も復習しておく つぎに有名なオイラーの公式 eiθ cosθ isinθ θは実数 をヒントにして複素数z の指数関数ez を定義. 突然ですが皆さんはネイピア数 e 2718の 01 乗がいくつか分かりますか ではsin01 はどうでしょう パッと答えるのは難しいですよね 数の世界にはこのように指数関数三角関数など計算が複雑な関数が少なくありません. 三角関数の定義 三角関数とは以下で定義される sin θ cos θ tan θ sinthetacosthetatantheta sin θ cos θ tan θ のことです sin θ sintheta sin θ とは単位円上の 角度 θ theta θ に対応する点 の.
1 でない正の実数 a および正の実数 x に対し を満たす実数 p がただ一つ定まる この p を x の a を底とする対数として定義する x に対して a を底とする対数を log a x と表わせば上記の.

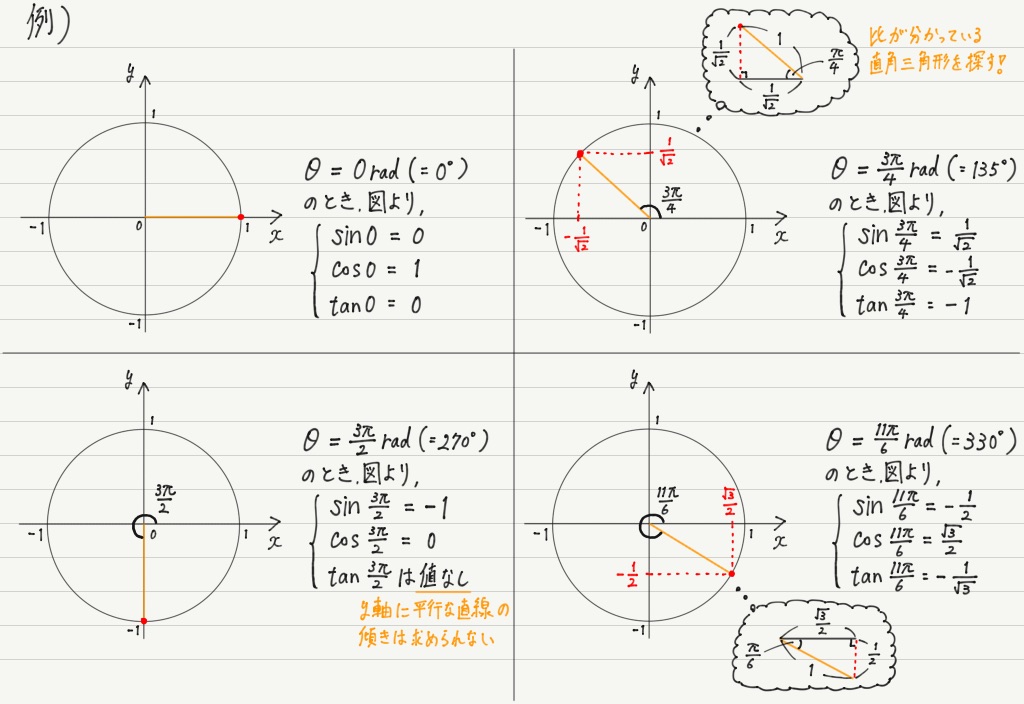
有名角 準有名角のsin Cosの値 一覧 理系のための備忘録
三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に

逆三角関数 Arcsin Arccos Arctan の定義と諸性質まとめ 数学の景色

ある三角関数の加法定理の図形的な証明 身勝手な主張
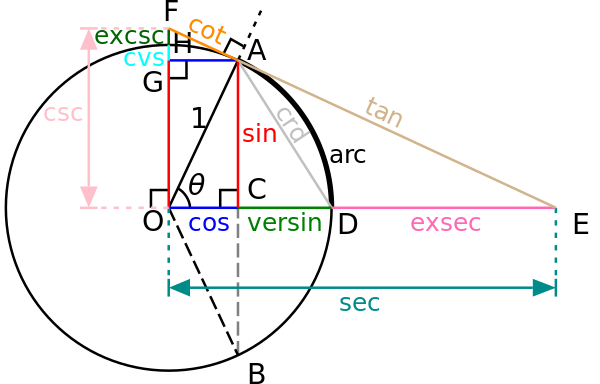
大学受験数学 三角関数 公式集 Wikibooks
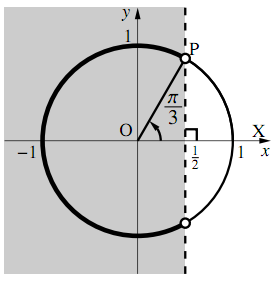
三角関数の定義 数学ii フリー教材開発コミュニティ Ftext
三角関数にて 以下の画像の公式を加法定理を用いず 且つ厳密に証明するとな Yahoo 知恵袋
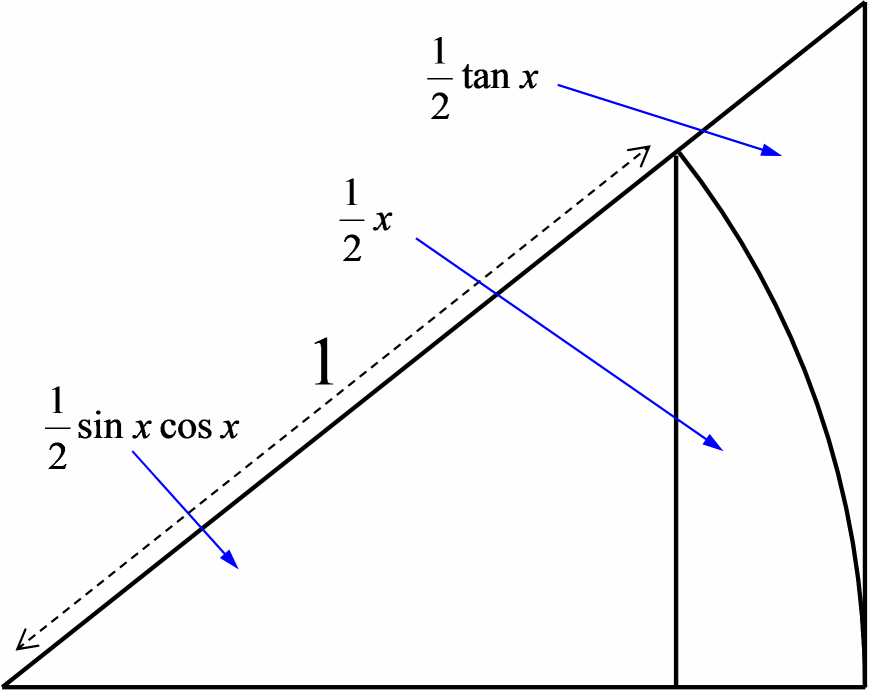
ロピタルの定理と三角関数の微分 数学 C 未確認飛行 C
You have just read the article entitled 三角 関数 定義 厳密. You can also bookmark this page with the URL : https://gracies1ji.blogspot.com/2022/06/blog-post_783.html
0 Response to "三角 関数 定義 厳密"
Post a Comment